Not easy to dig deeper when life is busy but I’ll try to share the beginning of an answer the most clearly possible…
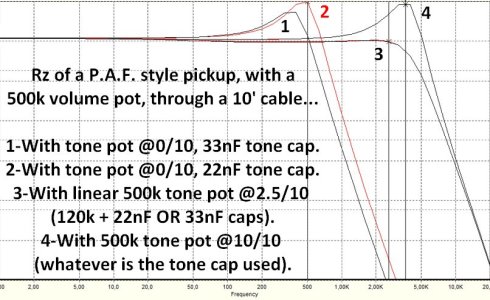
a)About frequencies: with a typical P.A.F. style humbucker like the pickup involved in my previous posts, pickup inductance + capacitance of the tone cap (without resistance in between) sets the resonant peak around 500hz for a 22nF cap and 400hz for a 33nF one. 3.5khz to 3.75khz is the resonant frequency of the pickup as set only by its inductance + cable capacitance (when the tone control is @ 10/10 and meant to keep the tone cap out of the circuit). With a resistance of 120k, the tone network drags the maximum output of the pickup between the frequencies mentioned and more precisely, around 2.5khz (although the “resonant peak” looks more like a “dome” with a so low resistive load).
b)No 33nF Orange Drop here. But our tests involved things like a 33nF ceramic cap and it didn’t shape the harmonic spectrum like the 33nF PIO evoked above: no correlation has been found between measured capacitive values and frequency selective behavior.
c)Now, as a matter of fact, a resistive load + cap doesn’t necessarily appear to filter harmonics in the same way than a resistive load alone, and i also see something interesting in this apparent paradox.

More later maybe: it’s late at night here, my bed is calling me. ;-)
...I EDIT this message to complete it quickly, before a working day.
Below is a 5spice sim illustrating my tedious explanation a) above. One can see how 33nF or 22nF caps make a clear difference for the resonant peak of a generic humbucker with a tone pot @0/10 (peaks 1 & 2), no difference at all with a 500k tone pot @ 10/10 (peak 4) and an almost imperceptible difference when the resistive load of the tone control is 120k (=a linear 500k set @ 1/4, peak number 3; the red and black lines reffering to 22 or 33nF caps don't overlay exactly but the difference is minuscule).
The distribution of electrically generated harmonics SHOULD follow these curves at least approximatively and with consistency. A tone pot set @ 120k SHOULD filter the harmonics in the same way whatever is the tone cap used. In experimental reality (ours, at least), it's not the case (regardless of the capacitive value of components and of the related phase shift). That's precisely why i've shared harmonic measurements above.