L
Little Pigbacon
Guest
Re: A pickup physics questions
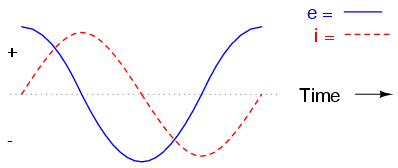
Well, because the (j) component doesn't dissipate energy into a non-electrical form (again, in an ideal circuit element, lumped-parameter approximation, etc.), and because it's frequency dependent, the ohm value along the (j) axis -- and the magnitude impedance -- are only meaningful at a frequency for our purposes, since we're usually not doing time-domain analysis. But the energy "loss" is imaginary; you get it back later. It's only in a purely resistive (j = 0) circuit element that energy leaves the circuit in our simple RLC textbook example. So "kinda, but not really".
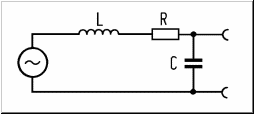
But yeah, anyone wanting to know more should grab a book. I don't really do phasor math anymore, and we like thinking about real pickups here. And playing them. One parting thought, though: You can usually get a pretty good idea of what's going on in a guitar circuit by looking at pretty simple circuit models based on resistors, inductors, capacitors. As uOpt said, it's mainly simply filters. The trick is remembering that some of the elements are best thought of as combinations of basic circuit elements. For example, a pickup could be thought of as an inductor in series with a resistor, with a capacitor in parallel. Connects to a resistor in parallel (that's your volume control) with a voltage divider wiper, which might connect to another resistor-wipey-thing with a capacitor (depending on how you wire it). A cable is a resistor with a small inductor in series and a capacitor in parallel. The input of an amp might be a resistor with a capacitor in parallel. (There are lots of parallel capacitances in our world; they naturally occur in a lot of the things we build and use, in addition to the actual capacitors that we put in them.)
Sure, but it is the resistance or losses due to the stuff in the circuit (whatever it happens to be). It is measured in ohms because it is virtually the same thing even if it originates from inductive and capacitive losses. The imaginary part (j) is where reactance comes in and affects phase.
Well, because the (j) component doesn't dissipate energy into a non-electrical form (again, in an ideal circuit element, lumped-parameter approximation, etc.), and because it's frequency dependent, the ohm value along the (j) axis -- and the magnitude impedance -- are only meaningful at a frequency for our purposes, since we're usually not doing time-domain analysis. But the energy "loss" is imaginary; you get it back later. It's only in a purely resistive (j = 0) circuit element that energy leaves the circuit in our simple RLC textbook example. So "kinda, but not really".
But yeah, anyone wanting to know more should grab a book. I don't really do phasor math anymore, and we like thinking about real pickups here. And playing them. One parting thought, though: You can usually get a pretty good idea of what's going on in a guitar circuit by looking at pretty simple circuit models based on resistors, inductors, capacitors. As uOpt said, it's mainly simply filters. The trick is remembering that some of the elements are best thought of as combinations of basic circuit elements. For example, a pickup could be thought of as an inductor in series with a resistor, with a capacitor in parallel. Connects to a resistor in parallel (that's your volume control) with a voltage divider wiper, which might connect to another resistor-wipey-thing with a capacitor (depending on how you wire it). A cable is a resistor with a small inductor in series and a capacitor in parallel. The input of an amp might be a resistor with a capacitor in parallel. (There are lots of parallel capacitances in our world; they naturally occur in a lot of the things we build and use, in addition to the actual capacitors that we put in them.)
Last edited: